Tumor localization using fundus view photography for episcleral plaque therapy
Michael D. C. Evansa, Melvin A. Astrahanb, and Rosario Batec
Medical Physics, 20(3), pp. 769-775, Copyright 1993 Am.Assoc.Phys.Med.
(a) Medical Physics Unit, McGill University, Montreal, Canada
Reprint requests: Medical Physics, Montreal General Hospital, 1650 Cedar Ave., Montreal, Quebec, Canada H3G IA4.
(b) Department of Radiation Oncology, University of Southern California, Kenneth Norris Cancer Center, 1441 Eastlake Ave, Los Angeles, California, 90033.
(c) Department of Ophthalmology, Royal Victoria Hospital, Montreal, Canada.
ABSTRACT
The accurate localization of ophthalmic tumors on the scleral surface is important when calculating radiation dose to the tumor and adjacent structures from episcleral I-125 plaques. This is particularly true for tumors close to the fovea or optic nerve. A fundus view diagram of the eye is often used by ophthalmologists to describe the size and shape of the tumor perimeter as well as its geographical location on the retinal surface. There is, however, an inherent inaccuracy associated with the use of a hand drawn diagram to obtain physical measurements. A computer planning program has been developed which uses CT and a digitized photographic montage of the posterior hemisphere to estimate the size and location of posteriorly located tumors. A simple phantom was constructed to test the software and a direct comparison made between planned versus measured tumor size and location in an excised eye.
Key words: ophthalmic plaque, fundus photography, choroidal melanoma
(Received 22 November 1991; accepted for publication 4 March 1993)
I. INTRODUCTION
Removable episcleral plaques are often used in the treatment of ophthalmic tumors, including choroidal melanoma (1-5). The accurate delineation of the tumor perimeter on the retinal surface is important in performing radiation dosimetry with respect to the tumor and various adjacent structures. It permits selection of the most appropriately sized plaque to cover the tumor with the required margin and enables optimization of treatment for tumors close to the fovea or optic nerve (6,7). Accurate tumor localization and preplanning also benefits the surgeon by providing (nominal) coordinates of the plaque's suture eyelets with respect to various anatomic landmarks.
The fundus diagram of the eye is often used by ophthalmologists to indicate the size and shape of the tumor perimeter as well as its geographical location on the retinal surface. The fundus diagram is a method of projecting (or mapping) a spherical surface onto a plane. Another method which is perhaps more familiar is Mercator's projection, typically used to depict the Earth's surface. When a curved surface is projected onto a plane, objects are geometrically distorted, the nature of the distortion depending on the method of mapping. The method of projection is usually chosen so as to minimize distortion in the region of greatest interest. In Mercator's projection, geometric distortion is least at the equator and increases as one approaches the poles. In the fundus diagram, geometric distortion is least near the posterior pole of the eye (fundus region) and increases as one approaches the anterior pole.
Since geometric distortion on the fundus diagram increases with distance from the posterior pole, it is difficult to hand draw a tumor perimeter in such a way that it can be correctly mapped back to a spherical surface. The magnitude of error can be expected to increase as tumor distance from the posterior pole increases.
In addition to the fundus diagram, the ophthalmologist will generally take a series of photographs of the fundus region. A special camera is used which photographs the retina through the lens of the eye. These photographs have a certain kinship to the fundus diagram since they are also a projection of a portion of the retinal surface onto a photographic plane. Computer software has been developed (6,7) which enables the tumor perimeter and other anatomic landmarks to be estimated from these photographs. Although the photos are subject to additional distortions associated with the camera optics and image transmission through the vitreous and lens of the eye, the resulting error is expected to be small compared to the use of a hand drawn diagram to localize the tumor.
The planning software has certain limitations resulting from the image digitization process and various assumptions made in the programming. A simple phantom was constructed to assess the accuracy of this software in measuring the size of a known area at different positions in the posterior hemisphere. Tumor location derived from an actual clinical planning exercise was subsequently compared to direct measurement on an excised eye.
II. THE FUNDUS DIAGRAM
|
As we have defined it, the fundus diagram is a projection of a spherical surface extending from the posterior pole to the limbus. A transverse slice of the right eye is shown in the upper portion of Fig. 1, and the camera icon indicates the direction of view. At the center of the diagram is the posterior pole. With respect to this center, radial distance (R) is directly proportional to arc length along a retinal meridian. Distance measured circumferentially is also proportional to arc length, but the scaling factor is a function of R rather than constant. The schematic representation of this surface is shown in the lower half of Fig. 1 as a series of three concentric circles in the coronal plane which correspond to anatomical regions of the eye.
The innermost circle represents the equatorial circumference in the coronal plane, and the interior surface of the eye from the equator to the posterior pole is contained within this circle. Even though this is the smallest circle, its diameter represents the largest chord length in the drawing. This region contains the optic disc, where the optic nerve passes through the sclera, as well as the macula (which surrounds the fovea) which is the region of greatest optical acuity found at the posterior pole of the eye.
|
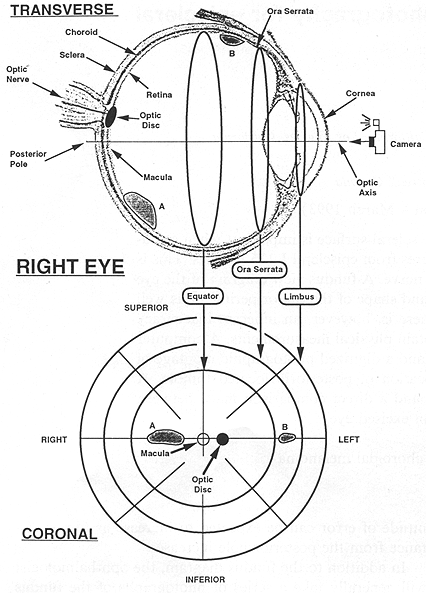
FIG. 1. The anatomy of the right eye in a transverse cut relates to the fundus view diagram. Two tumors labeled A and B located on a transverse great circle are shown in both views.
|
The next largest circle represents the circumference in the coronal plane at the ora serrata, which is the point at which the retina terminates at the cilliary body. The region contained between this circle and the equator represents a band on the inside surface of the eye from the equator to the ora serrata. The outermost circle in the fundus diagram is the circumference in the coronal plane at the limbus, which is the point at which the sclera terminates at the cornea. This circle, although apparently the largest on the diagram, actually represents the smallest diameter of the three.
As the central point of the diagram represents the posterior pole of the eye, any radial displacement from this point represents a shift in the anterior direction along a retinal meridian, so that the most anterior position of the diagram is reached at the outermost circle. The clock position of the tumor also gives geographic information with respect to the coronal plane of the patient, so that 12 o'clock is superior, 6 o'clock is inferior, 3 o'clock is to the patient's left, and 9 o'clock is to the patient's right. The location of the optic nerve is indicated by a small solid circle along the 3 to 9 o'clock line (90* meridian). As the optic nerve lies medially to the macula, the position of this solid circle identifies the right or left eye. In the upper half of Fig. 1 the eye is shown containing two tumors labeled A and B and their corresponding positions in the fundus diagram are also shown. As tumor A lies in the posterior hemisphere on the right side, it is contained entirely in the smallest concentric circle of the fundus diagram. Tumor B lies on the left of the optic axis between the equator and the ora seratta, thus it is located between the smallest and middle circle on the fundus diagram.
III. FUNDUS PHOTOGRAPHY
Fundus view photography is often performed to aid in the diagnosis and localization of posterior tumors. The procedure typically takes 20 min, and is routinely performed in the ophthalmology clinic. With the use of a specialized fundus camera and immobilization device, photographs are taken through the patient's dilated iris in the direction of the posterior pole. The eye is rotated by following a target light with the fellow eye, so that the clinically relevant portion of the posterior pole and periphery is brought into the field of view of the camera. From these images a composite or montage view is obtained by superimposing the major blood vessels which are common, starting from the optic nerve and moving to the periphery in all directions so that an extended view of the posterior surface of the eye is obtained.
As the maximum opening of the dilated iris is significantly smaller than the diameter of the eye, the field of view of the camera is limited to regions posterior to the ora seratta in the vicinity of the equator, so that photographs of the anterior hemisphere of the eye are unobtainable. However, as the choroid ends at the ora seratta, the majority of choroidal melanomas will be contained in the posterior hemisphere of the eye which makes the montage useful in establishing the location of these tumors.
IV. MATERIALS AND METHODS
A dedicated episcleral plaque treatment planning computer program has been developed by Astrahan et al. (6,7) at the University of Southern California (USC) which uses CT, ultrasound, and fundus view photography to noninvasively estimate the size and location of a tumor on the retinal surface. A simple eye phantom was developed at McGill University to test this software in the laboratory. A standard ping-pong ball (Champion, Model 125, Guangzhou, China) with a 37.7 mm diameter was sliced in half along its equator so that two hemispheres were produced. A 15.3 mm diameter hole, representing the limbus, was punched out over the pole of one hemisphere. A 60 mm cross with tick markings every 5 mm was centered over the pole of the other hemisphere and placed along orthogonal great circles of the phantom. When the two halves of the phantom were secured together the dimensions were similar to a human eye with the cross lined up over the posterior pole corresponding to the macula.
An analogy can be drawn between a globe of the Earth, and a fundus view of the eye. Looking from the South to North pole, the surface of the entire Northern Hemisphere would be seen inside the first circle, the Earth's surface from the equator south to the tropic of Capricorn would lie inside the middle band, and the region from the Tropic of Capricorn to a latitude of 65° south would be in the outer band. The Earth's surface from 65° south to the South Pole would be excluded. Continental distortion will vary with the distance from the center of the diagram in this projection in a similar manner to the equal azimuthal projection of the Earth used by the United Nations. To carry the analogy of the globe one step further, a map of the land mass from the equator, north along the 90° west longitude through North America, over the North Pole and south along the 90° east longitude through Eurasia to the equator was placed inside the phantom. Three 14 mm X 7 mm acetate ellipses were placed inside the posterior hemisphere to simulate arbitrary positions of choroidal tumors. The first ellipse was placed at the posterior pole corresponding to the North Pole, the second ellipse was placed at a latitude of about 45° and arbitrarily rotated to cover much of North America, and the third ellipse was centered along the 180° longitude at a latitude of about 15° corresponding to a region south and east of Hawaii.
The phantom was placed on the chin rest of a fundus camera (RC-Xv, Kowa Company Ltd., Japan) and was accommodated for height and distance in relation to the camera's objective lens. With a 45° angle of view, five fields were photographed starting from the center of the cross and following the tick marks in both the vertical and horizontal directions. By combining the central field at the posterior pole with that of the periphery along the two major axes, a montage of much of the posterior hemisphere was produced. A typical set of clinical photographs would concentrate on a somewhat smaller surface area including only the tumor, fovea, optic disc, and regions inbetween.
This montage was then digitized by the treatment planning computer. The physical dimensions of the eye used by the computer program (normally obtained from CT in patients) were set to correspond to the physical dimensions of the phantom. The computer software permits a "standard" tumor with an elliptical perimeter to be created algorithmically using parameters for major and minor diameters, latitude, longitude, rotation, and height of the tumor on the retina. Such a 14 mm X 7 mm "standard" tumor was created and overlayed over each digitized tumor.
Clinical testing was performed at USC. A patient who had been planned for plaque therapy (using CT, ultrasound, and fundus photography) was found to have scleral extension of the tumor, thereby making the patient ineligible for plaque therapy. Immediately following enucleation direct measurement of eye size and tumor location relative to the optic nerve and limbus was performed. These measurements were compared to values derived from the treatment plan.
V. RESULTS AND DISCUSSION
The program calibrates and orients the fundus montage by requiring the user to place markers over the fovea and optic disc, and entering the chord distance between the centers of these landmarks. This distance can be estimated from CT scans of the patient's eye, optic disc diameters, or even a generic value can be used. In this experiment the optic nerve was considered to be at the first tick mark from the optical axis of the phantom, and this distance was known to represent an arc length of 5 mm.
|
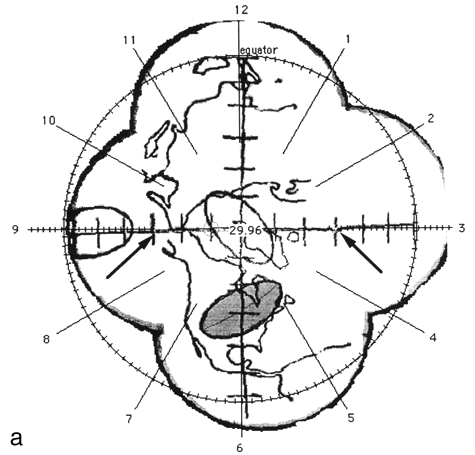
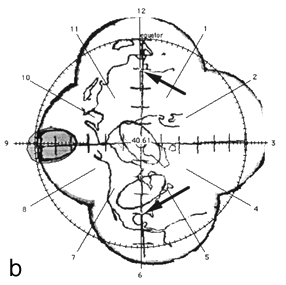
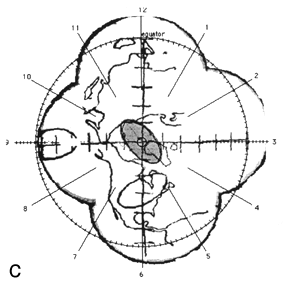
FIG. 2. The photographic montage of the posterior hemisphere of the ping-pong ball phantom with the grid system centered over the posterior pole, test ellipses, and world land masses. The three figures depict the locations studied. The 14 mm X 7 mm ellipses drawn by the computer are shown in grey at 45° (a), the equator (b), and at the pole (c). The distance in mm (arc length) between the ends of the ruler is indicated by the arrows.
|
|
|
Figure 2 shows the digitized montage of the posterior hemisphere with the grid system, map of the land mass, and three test ellipses. The equator has been placed by the computer, and the clock positions around the circumference are also shown. Using the computer software, 14 mm X 7 mm "standard" tumors (shaded in grey) were centered over the digitized ellipses. The size of the digitized ellipses at 45° latitude [Fig. 2(a)] and at the pole [Fig. 2(c)] where circumferential geometric distortion is small matched the "standard" tumors almost exactly. Near the equator [Fig. 2(b)], however, the digitized tumor appears smaller than the "standard." This is because the montage is not corrected for circumferential geometric distortion. When the tumor perimeter is subsequently traced from this image the software will attempt to correct for this as discussed in Appendix A.
A distance measuring tool provided by the software allows the digitization of known distances to be assessed. For example, in Fig. 2 (a) the arc length between seven tick marks along the horizontal line, indicated by arrows was given as 29.9 mm using the measuring tool in comparison to the known value of 30 mm. In Fig. 2(b) the arc length between nine tick marks along the vertical line, indicated by arrows was given as 40.6 mm in comparison to the known value of 40 mm.
These measurements indicate the magnitude of error introduced by the fundus camera and video digitizing process to be quite small. Since the photographs of the phantom were taken without a cornea, lens, and vitreous humour, optical distortion resulting from image transmission through these structures has not been included. Furthermore, the fovea-to-optic disc calibration distances was a precisely known value. The above results, therefore, represent the minimum error to be expected in the planning process. In clinical practice, the errors can be expected to be more apparent, primarily resulting from uncertainty in the fovea-to-optic disc calibration distance and the eye being an imperfect sphere.
The program is also useful even when fundus view photographs are not available, as the hand drawing of the fundus can be entered in place of the photos, corrected for circumferential distortion, and dimensions obtained from
ultrasound or other measuring methods can be entered to improve the localization process.
A comparison of preplanned versus postenucleation measurements is presented in Table 1 for a small, nominally circular tumor located about midway between the posterior pole and equator. Physical dimensions of the eye derived prior to surgery from digitized CT films were found to be within 0.5 mm of the dimensions measured postenucleation. We consider this accuracy sufficient for treatment planning purposes.
TABLE 1. A comparison between distances calculated from the treatment plane and distances obtained by direct measurement of the excised eye.
Site
Anterior to posterior
Equatorial diameter
Limbus diameter
Optic nerve edge to tumor perimeter
Limbus to tumor perimeter
Tumor diameter
Limbus to plaque eyelet
|
From
treatment plan
26 mm
27 mm
12.5 mm
6 mm (a)
16.4 mm (a)
3.6 mm (a)
9.5 mm
|
Measured
externally
25.5 mm
26.5 mm
12.5 mm
7 mm (b)
15.5 mm (b)
4.5 mm (b)
9.5 mm
|
(a) Calculated on the retinal surface.
(b) Measured with respect to external scleral extension of tumor.
The diameter of the scleral extension of the tumor was about I mm larger than the retinal diameter derived from the fundus montage. Estimated chord length between the retinal perimeter of the tumor and optic disc was almost 1 mm smaller than the chord measured between the penimeter of the scleral extension and the optic nerve. This difference is about what one would expect owing to the larger spherical radius of the external sclera compared to the retina. The estimated chord length between the retinal perimeter of the tumor and the limbus was about 0.9 mm greater than the chord measured between the perimeter of the scleral extension and the limbus. The plaque intended for this patient has a positioning notch which is placed against the optic nerve and two anterior suture eyelets as depicted in Fig. 3. With the plaque in the prescribed position, the distance from the most anterior eyelet to the limbus was both measured and calculated to be 9.5 mm. These results indicate that localization accuracy is on the order of 1 mm in clinical practice which is consistent with the USC experience. It would appear that distortions resulting from image transmission through the vitreous, lens, and cornea are small and can probably be ignored for treatment planning purposes.

|
FIG. 3. A small tumor of nearly circular perimeter is located at about 1 o'clock, midway between the posterior pole and equator of a right eye. Also plotted are portions of the major blood vessels emanating from the optic disc, the plaque perimeter, and source locations within the plaque projected onto the retina, and isodose contours on the retina normalized to the tumor apex. Tic marks represent 1 mm of arc.
|
VI. CONCLUSION
Accurately determining the size and location of ophthalmic tumors is important when performing 1-125 plaque dosimetry and can be of great assistance for surgical planning as well. A localization technique which uses CT images, a digitized montage of fundus camera photographs including the tumor, fovea, and optic disc, and computer software to integrate the two has been developed. A simple phantom was devised to assess the technique. The results were found to be acceptable for theoretical tumors located within the limits of fundus view photography (which represents the majority of choroidal melanomas). A comparison between preplanned and postenucleation measurements of tumor and plaque location indicates the technique to be sufficiently accurate for treatment planning purposes.
ACKNOWLEDGMENT
The technical assistance and generous loan of computer time by C. Pla is gratefully acknowledged.
APPENDIX
A semiquantitative method of tumor localization based on CT imaging and fundus photography has been developed by Astrahan et al. (Refs. 6 and 7). Several simplifications and assumptions are incorporated into this approach. Although eyes are not perfectly spherical, experience in developing the treatment planning system suggested that the posterior region of most eyes could be approximated as a hemisphere, The anterior portion of the eye is modeled as an oblate spheroid which intersects the posterior hemisphere and a spherical segment representing the cornea. The treatment planning system uses interactive graphics superimposed on CT images to find a combination of hemisphere, oblate spheroid, and spherical segment which closely approximates the eye of interest. The intersection of the hemisphere and oblate spheroid is defined to be the equator and thus localizes the "center" of the eye. The next simplification is to consider the entire retinal surface of the eye to be spherical, even that portion anterior to the equator. The result is that localization of anterior tumors is somewhat less precise than posterior tumors.
Since the retinal surface of the eye is considered to be spherical, a fundus camera photograph of about 40° field of view is fundamentally similar to the central region of a fundus diagram. Each is a projection of a portion of a spherical surface onto an imaging plane with the center of the photograph being equivalent to the center of a fundus diagram where geometric distortion is minimum. Since the field of view is small, circumferential distortion at the periphery of each photograph compared to its center will be fairly small.
A "best-fit" montage of these photographs which includes the tumor perimeter, optic disc, macula, and region in between is assembled by superimposing anatomic landmarks such as the major blood vessels. This montage can be assembled manually from photographic prints and subsequently digitized as a group, or the component images may be digitized individually and the montage created on the computer (Adobe Photoshop). Digital assembly is particularly helpful if some of the photographs were taken at different magnifications, since it is possible to interactively rotate, translate, and scale the images on the computer.
Once the fundus montage has been digitized, markers are interactively superimposed over the fovea (center of the macula) and optic disc. Ideally, the fovea should be at the center of one of the photos and the optic disc should be visible on the same photo. The fovea is defined to be at the posterior pole and the center of the optic disc is defined to lie on the 90° retinal meridian (Ref. 6) so this pair of markers simultaneously establishes the rotational orientation of the montage about the anterior-posterior (X) axis of the eye and the radial scaling factor. The distance between the markers on the montage is considered to be directly proportional to a radially oriented arc length on the retinal surface since the line between them is, by definition, the projection of a segment of a meridian. The actual arc length between the fovea and optic disc is estimated from the radius of the retinal sphere and the angle between the posterior pole, center of the eye, and the optic nerve as obtained from CT. Thus, points of interest on the montage can be defined in terms of arc length from the posterior pole and circumferential "clock position" relative to the 90° meridian.
In reality, however, the fundus camera redirects its angle of view for each photograph and the centers of individual photos should really be considered the equivalent of local "posterior poles." Consider an ideal photograph in which the center of a tumor near the equator was at the center of the photograph. This picture would be identical (except for distortions resulting from transmission through the lens of the eye) to one in which the camera had been centered on the posterior pole and the same tumor surrounded posterior the pole! If this ideal photograph was part of the montage, the radial arc length (R) between the
posterior pole and center of the tumor, and the "clock position" of a meridian (φ) which passes through the posterior pole and the center of the tumor can be obtained from the montage. Three-dimensional (3D) Cartesian coordinates of the center of the tumor are easily derived from(R,φ). On this ideal photo, however, circumferential geometric distortion of the tumor perimeter would be very small, a function of radial arc length from its own local center, whereas it really should be quite significant (being near the equator), a function of radial arc length from the posterior pole. An attempt to correct this situation is made by calculating Cartesian coordinates for points defining the tumor perimeter as if the camera had been centered on the posterior pole and the tumor center coincided with the posterior pole. Proper rotational orientation of the perimeter with respect to its own center is maintained by noting where the perimeter crosses the φ meridian (since there is no circumferential distortion along a meridian). A matrix is then calculated which rotates the "posterior pole" to R,φ and this matrix is also applied to the tumor perimeter. The result is that we have a set of 3D Cartesian points which closely approximate the tumor perimeter where it intersects the retina and which can now be mapped back onto the fundus diagram.
The process is reasonably valid even if the fovea is not at the center of an image and/or the fovea and optic disc happen to lie on adjacent photos since the distance between the pair is small (4 to 5 mm) and the field of view is small. This applies to the tumor as well, in which the center of a composite tumor is simply considered to correspond to the center of a single image.
Transformation subroutines (in the C programming language) between 3D Cartesian coordinates and 2D Cartesian coordinates relative to the center of a fundus diagram are outlined below for a coordinate system in which the center of the eyeis the origin and the positive X axis passes through the anterior pole (Ref. 6). The first subroutine accepts 3D Cartesian (x,y,z) coordinates and returns horizontal and vertical (h,v) coordinates relative to center (posterior pole) of a fundus diagram. The second routine is the reverse transformation. The special case of the posterior pole itself is handled by an explicit test.
Global variables:
retinaRadius = radius of sphere which approximates the retina.
scleraRadius = estimated to be 1mm outside the retina.
limbusRadius = half the measured diameter of limbus.
diagramRadius = radius of limbus circle on fundus diagram (in pixels);
limbusAngle = 180.0 - (asin(limbusRadius / scleraRadius) * (180.0/pi));
fDfactor = (diagramRadius / limbusAngle) * (180.0/pi);
void Convert3DtoFD(float x, float y, float z, float *h, float *v)
{
float f;
if ((y == 0) && (z == 0))
{ *h = 0;
*v = 0;
}
else { f = (fDfactor - acos(-x / retinaRadius)) / sqrt((y * y) + (z * z));
*h = y * f;
*v = z * f;
};
}
void ConvertFDto3D(float h, float v, float *x, float *y, float *z)
{
float a,s,arcLength;
if ((h == 0) && (v == 0))
{ *x = -retinaRadius;
*y = 0;
*z = 0;
}
else { arcLength = sqrt((h * h) + (v * v));
a = arcLength / fDfactor;
*x = -retinaRadius * cos(a);
s = (retinaRadius * sin(a)) / arcLength;
*y = s * h;
*z = s * v;
};
}
REFERENCES
- S. Packer, M. Rotman, R. G. Fairchild, D. M. Albert, H. L. Atkins, and B. Chan, "Irradiation of choroid melanoma with iodine 125 ophthalmic plaque," Arch. Ophthalmol. 98, 1453-1457 (1980).
- L. S. Brady, J. A. Shields, J.J. Augsburger, and J. L. Day, "Malignant intraocular tumors," Cancer 49, 578-585 (1982).
- J. Earle, R. W. Kline, and D. M. Robertson, "Selection of iodine 125 for the collaborative ocular melanoma study," Arch. Ophthalmol. 105, 763-764 (1987).
- S. Packer, "Iodine-125 radiation of posterior uveal melanoma," Oph
thalmology 94, 1621-1626 (1987).
- B. R. Garretson, D. M. Robertson, and J. D. Earle, "Choroidal melanoma treatment with iodine 125 brachytberapy," Arch. Ophthalmol. 105, 1394-1397 (1987).
- M. A. Astrahan, G. Luxton, G. Jozsef, T. D. Kampp, P. E. Liggett, M. D. Sapozink, and Z. Petrovich, "An interactive treatment planning system for ophthalmic plaque radiotherapy," Int. J. Radiat. Oncol. Biol. Phys. 18, 679-687 (1990).
- M. A. Astrahan, G. Luxton, G. Jozsef, P. E. Liggett, and Z. Petrovich, "Optimization of 1-125 ophthalmic plaque brachytherapy," Med. Phys. 17, 1053-1057 (1990).
Plaque Simulator References |
Guide Contents




