Measurement of Dose Rate from Exposure-Calibrated I-125 Seeds

Dose rate in water 1 cm transverse to an I-125 seed calibrated for air kerma strength is not well established; I-125 dosimetry calculations are, however, based on this constant. The specific dose constant was obtained from a series of dose rate measurements using thermoluminescent dosimetry (TLD) in a rigid geometry, full scatter acrylic phantom for individual model 6711 seeds. With a statistical precision of approximately ±.5%, the dose rate to an infinitesimal mass of water located in acrylic at a perpendicular distance of 1 cm from the seed was found to be 0.977 cGy/h per μGy-m²/h of air kerma strength. Dose rate in a water phantom was calculated using a model that takes into account differences in both attenuation and scatter between water and acrylic. The specific dose constant in water was determined to be 0.932 (1.184 cGy-cm²/mCi-h, for the conventional exposure rate constant of 1.45 R cm²/mCi-h). This value is 7.5% less than dose rate in water from an unattenuated point source, and 9.7% less than the value commonly used for dosimetry calculations. The results suggest that most clinical I-125 dosimetry estimates to date should be reconsidered for a possible reduction by about 10%. Relative scatter attenuation factors at 3 and 5 mm are also presented.

There are significant potential advantages to the use of I-125 in certain brachytherapy procedures compared to the use of more traditional isotopes such as Co-60, Ra-226, Ir-192, Au-98 and Cs-137. The advantages are associated with the low energy (energy-weighted mean approximately 28 keV) of I-125/Te-125 x- and gamma rays. Low energy radiation considerably reduces the problem of personnel shielding, and decreases the dose to critical normal tissues both adjacent to and distant from the target region. The gains, however, are accomplished at the expense of an increase in dosimetric complexity and uncertainty. Severe anisotropy (13,16,17), loss of backscatter (19,25) and tissue type dependence (7,9) contribute to dose rate uncertainty in clinical applications.

There remains uncertainty in the dose rate from I-125 seeds in a phantom from even a single seed calibrated by exposure rate in air, or equivalently, air kerma strength (1). Krishnaswarny (13), for example, measured a value 21% less than previous measurements at I cm from a single I-125 seed of a design similar to the discontinued model 6701 (Models 6702 and 6711 I-125 seeds are manufactured by 3M Corp., Medical-Surgical Products, New Brighton, MN.). Subsequent measurements (10,16,17) and calculations (5,6) have elaborated the 2-dimensional relative dose rate distribution around the currently utilized models 6702 and 6711 seeds of I-125. Examination of the published literature (10,13,16,17,24,25,26) shows, however, a sparsity of precise absolute dose rate measurement within 10 mm of a seed. Dose rate in this region is particularly necessary for specification of dose to the retina, sclera and apex of a tumor in ophthalmic plaque radiotherapy for uveal melanoma, and may be of significance in comparing the results of treatment with I-125 plaques to traditional Co-60 applicators. The present work is an effort to provide absolute dose rate measurements in acrylic with a high degree of statistical precision near an exposure-calibrated model 6711 seed of I-125 . Dose rate measured in acrylic will be related to dose rate in water using a calculational model that takes into account differences in attenuation and scatter between water and acrylic.

A polymethyl methacrylate (PMMA or "acrylic"-C₅H₈O₂) phantom constructed from rectangular blocks (Fig. 1) was used for all I-125 measurements. A removable 5.3 X 5.3 X 1.3 cm section located at the center of the phantom was drilled with a hole 1 mm in diameter for a model 6711 I-125 seed (diameter 0.8 mm, total length 4.5 mm, active length 3 mm). Parallel holes were drilled to position 1 mm diameter X 3 mm length cylindrical lithium fluoride (LiF) thermoluminescent dosimeter (TLD) detectors (TLD-100 (LiF) supplied by Harshaw/Filtrol, Solon, OH) in a circular pattern centered about the seed (Fig. 2). TLD's were aligned with their centers at the same depth as the center of the seed. The 1 mm diameter X 6 mm length void at one end and the .5 mm diameter X 4 mm void at the other end of each TILD were not plugged. Three blocks were used, with nominal radii .3, .5, and 1.0 cm for the circle of TLD's.

Fig. 1. Measurement phantorn consisting of'rectangular blocks. Central block contained the "I seed and TILD detectors. TLD's were arranged parallel to the seed in a circle.

Transverse distances between TLD's and I-125 seed were measured from radiographic films for each detector block. Metal markers 1 mm diameter, 2 mm length were placed in the 1 mm diameter TLD and seed slots and taped to adhere to the 5.3 X 5.3 cm surface, to denote seed and detector location. Film magnification was approximately 8:1. The mean distances center-to-center were measured to be 0.298 ±.002, 0.498 ±.003, and 0.999 ±.004 cm, respectively. Uncertainties are due to estimated errors in distance measurement on films (±.07 mm) and film magnification (±.35%).

TLD rods were initially sorted into groups of ±3.5% sensitivity (18). For each exposure to an I-125 seed the TLD's were taken from a single sensitivity group. Six to 10 additional TLD's from the same group were irradiated on the same day with a dose of 1 Gy (water) of 4 MV radiation for relative calibration. Precisely calibrated 4 MV irradiations are readily reproducible, enabling the beam to be useful for relative calibration of multiple measurements performed at different times. The 4 MV beam was calibrated using a polystyrene phantom, following the American Association of Physicists in Medicine Task Group 21 (AAPM TG-21) protocol (2). TLD's were annealed for 15 minutes at 105°C prior to readout. Each TLD group was annealed in its entirety for 1 hr at 400°C and 1 hr at 100°C before any re-use. Readouts from TLD's exposed to the I-125 seed were averaged, as were readouts from the group exposed to the 1 Gy of 4 MV radiation.

Dose rate in the phantom from the I-125 seed is referred to T_ref, the date of the seed calibration, according to Eq 1:

where T is the interval in days from T_ref to time of irradiation, R_I-125 is the mean TLD reading from the I-125 exposure, t is the duration in hr of the I-125 exposure, ^I-125C_4MV is the TLD sensitivity per unit dose (water) at I-125 energy relative to 4 MV, C_4MV is the mean TLD reading per Gy (water) at 4 MV, b is the average attenuation in the TLD as compared to acrylic, and a = log_e2/T_1/2 is the transformation constant for I-125. One Gy (water) is defined here as the x-ray fluence at a point that would correspond to a dose of 1 Gy being absorbed by an infinitesimal mass of water located at that point. T_1/2, the half-life of I-125 = 59.6 days, is taken from Kubo (14). I-125 half-life was also independently obtained from the present measurements by a least squares fit (23).

Fig. 2. Central 5.3 X 5.3 X 1.3 cm block, showing TLD locations arranged in a circle centered on the I-125 seed. Blocks with circle radii of .3, .5, and 1.0 cm were used. Cross section shows the centering of the 3 mm TLD's along the length of the parallel 4.5 mm physical length model 6711 I-125 seed. A small diameter hole extends through the 1.3 cm dimension of the block to enable ready removal of the seed and TLD detectors.

To obtain I-125 dose rate from TLD readings that are expressed in terms of sensitivity to 4 MV irradiation, the factor ^I-125C_4MV is required. TLD calibration per unit I-125 dose was approximated by TLD calibration per unit dose from an x-ray beam with an equivalent energy. An x-ray beam with parameters 70 kVp, 2.8 mm Al filtration, 2.4 mm Al first HVL was selected. The initial slope of the Al filter transmission graph corresponded to 2.1 mm Al HVL, equivalent energy 27.5 keV, which is close to I-125. Dose (water) from the x-ray beam was obtained rrom measurement of exposure, including a correction for the avcrage attenuation of the TLD, and then applying the factor for water (12) at 27.5 keV.

1. Measurement of exposure rate in an x-ray beam. Two 0.6 cm³ thimble ionization chambers of the same design were positioned parallel to each other, 8.5 cm apart in a 30 X 30 cm field as illustrated in Figure 3. Each chamber was connected to a digital electrometer. The two measurement systems had each been calibrated, 1 and 3 years earlier, for x-ray exposure in air at several beam qualities in this range at an Accredited Dosimetry Calibration Laboratory (M. D. Anderson Hospital and Tumor Institute ADCL, Houston TX). The system with the most recent calibration was used as reference, its calibration factor interpolated between ADCL-supplied values at 2.0 and 4.1 mm Al HVL. The ADCL values at the two x-ray beam qualities differed from one another by .9%.

Fig. 3. Setup for calibration of 70 kVp exposure of TLD's. Two calibrated ionization chambers determine relative exposure rate at nearby symmetric locations in a 30 X 30 cm 70 kVp x-ray field. Ionization chambers rest on rigid low-density foam blocks, simulating calibration conditions for ion chamber systems that have been exposure-calibrated at this energy in air.

The chambers were positioned 50 cm from the x-ray target, on a 50 cm thick stack of rigid foam blocks, density .03 g/cm³. The low-density rigid foam was chosen to provide a reproducible measurement environment with minimal backscatter, emulating ADCL calibration conditions. Ionization chambers were exposed for 5 min to an air kerma dose of approximately .3 Gy. Electrometer readings were corrected for instrument leakage, typically 1%. Probe positions were interchanged and the measurement repeated. In this way, relative exposure rate was obtained at the two locations, as well as relative sensitivity of the two measurement systems at this energy. The sensitivity of the second ionization chamber system was calculated with reference to the more recently calibrated system. The result was within .5% of the ADCL calibration that had been obtained 3 years earlier. One of the probes was now removed, and a group of TLD's substituted, as illustrated in Figure 4. The TLD's were given an air kerma dose of approximately .5 Gy. The remaining probe monitored the exposure.

Fig. 4. Setup for calibrated TLD exposure to 70 kVp x-ray beam. One of the ionization chambers of Figure 3 has been removed. The remaining probe monitors exposure rate at its location. The relative exposure rate at the TLD locations have been established by the setup Of Figure 3.

A test was devised to determine whether the presence of the monitor chamber (probe A) itself affected exposure rate at the location of the TLD's. TLD exposures occurred at the position formerly occupied by the second probe (probe B). Measurements were made from an x-ray exposure of both probes (A and B) with a third probe (C) present in a remote corner of the x-ray field. Probe A was now removed and another exposure recorded by measurement systems B and C. The ratio of readings B/C, with and without the presence of probe A, respectively, were compared. The ratios were in agreement to within 0.1%, indicating that the monitor probe (probe A) had negligible effect on the exposure experienced by the TLD's.

2. Comparison of 70 kVp X ray and 4 MV. Another set of TLD's from the same sensitivity group was irradiated with 1 Gy (water) of 4 MV radiation. The readouts from the calibrated 4 MV and 70 kVp irradiations then give the relative sensitivity of the TLD-100 per Gy (water) at 70 kVp, 27.5 keV equivalent energy, compared to 4 MV in accordance with Eq 2:

where R_70kVp is the mean TLD reading for the 70 kVp irradiation, M the temperature-pressure corrected ionization chamber reading, C the interpolated ADCL exposure calibration factor (given in Roentgen (R) per electrometer unit), X the relative exposure rate at the TLD position compared to that at the monitor, (including an inverse square correction factor of 0.988, introduced because the TLD's were 3 mm, more distant from the x-ray target than the central electrode of the ionization chamber), and 0.883 the water dose in cGy/R at 27.5 keV (12). The factor 0.974 corrects for the average x-ray fluence attenuation in the 1 mm diameter TLD itself (see following section). I-125 dose rate as measured and expressed by Eqs. 1-2 is the dose rate in water that would give the same TLD response as the x-ray fluence rate actually present in the acrylic phantom.

3. Attenuation by TLD in air. The average attenuation by the TLD was calculated, based on average chord lengths. The attenuation thickness for a photon passing through the TLD is 8D/3π, where D is the diameter. The mean effective attenuation thickness for a photon that interacts in the TLD is half of this, or 0.42 mm for the 1 mm diameter detectors. Compton scattering may be neglected in computing the correction factor because a Compton event at this energy results in an average loss of only 5% of the incident photon energy, and the recoil photon continues a traversal of the TLD. The calculation is simplified further by using mass energy absorption coefficients. These are interpolated from the tables of Hubbell (11) for a 27.5 keV photon in LiF, using a power law form E^-n, the photon energy E. The resulting attenuation in the TLD is 2.6%, leading to the 0.974 transmission factor in Eq. 2.

4. Attenuation correction for TLD in phantom. The presence of the LiF detector in the phantom perturbs the photon fluence at the reference point, primarily because the density of the crystalline LiF (2.7 g/cm³) is much greater than that of acrylic (1.18 g/cm³). Energy fluence and therefore dose rate is reduced. The dose rate reduction factor is approximated by the calculated ratio (of transmitted energy fluence) after interactions in 0.42 mm of LIF as compared to 0.42 mm acrylic at I-125 energy. For a 27.5 keV photon, energy absorption coefficients the ratio, b in Eq. 1, is 0.980.

lodine-125 seed calibration was certified by the manufacturer with 10 individual radiation measurements from the seed compared to the same measurements from a seed of the same design calibrated by the United States National Bureau of Standards. Four different calibrated seeds were obtained from the manufacturer over a period of 11 months, and used for the present study. The reference time was taken to be 12:00 noon local time at the factory on the date of calibration stated on the manufacturer's certificate.

Dose rate correction factors to account for the effect of the finite volume of the TLD detectors were calculated. The calculations are based on a model that treats the seed as an unfiltered line source with a "scatter-attenuation factor", that is, a factor that represents the effect of attenuation of primary and buildup of scatter radiation. For simplicity, the scatter-attenuation factor is taken to be dependent only on transverse distance from the seed, with no explicit angular dependence. This is motivated by the measurement geometry, in which the detectors are centered on the perpendicular bisector of the seed. Ling el al. (17) found empirically less than 5% variation in exposure rate as a function of angle for angles within 30° of the transverse direction.

The dose rate from the iodine seed in this model is written as

where D(x,y) is the dose rate (Gy/hr), y is the perpendicular distance (cm) from the line source of length L (cm), x is the parallel distance along the length of the seed (cm), S is the source activity expressed as air kerma strength (Gy-cm²/hr) and A(y) is a dimensionless scatter-attennation factor, that includes a factor to convert kerma rate in air to dose rate in water.

To correct for the finite dimensions of the TLD, the expression in Eq. 3 was averaged over the dimensions of the detector at each measurement distance by numerical integration (23). A(y) was assumed to be uniform over the dimensions of the TLD. The ratio of the dose rate for a point detector relative to the dose rate averaged over the TLD volume gives the correction factor for finite TLD size. These are given in Table 1 for the three measurement distances. Also given in Table 1 are adjustment factors based on the line source model to relate the results at measurement distances of 0.298, 0.498 and 0.999 cm to nominal distances of .3, .5, and 1.0 cm, respectively.

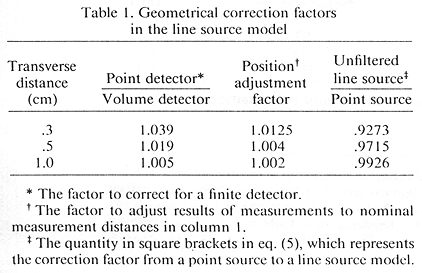
To relate the quantities used in point source and unfiltered line source model representations for dose rate along the perpendicular bisector of a seed, geometric factors are also given in Table 1. Thus, if dose rate is written in a conventional inverse square representation as in Williamson (27) as

D_o is the specific dose constant as defined by Williamson (27), and F(y) is dimensionless. The quantity in square brackets in Eq. 5 is tabulated at the measurement distances in the fourth column of Table 1. The quantity A(y) is closer to the concept of a scatter-attenuation factor for a point source than is F(y), since F(y) also includes the geometrical effect of the line source.

The use of TLD in a PMMA (acrylic) phantom measures its response to x-ray fluence at locations within the PMMA. To infer dose rate in water requires corrections to fluence rate due to differences in attenuation and scatter between PMMA and water. For example, at 30 keV the linear attenuation coefficient in PMMA is 4.4% less than water (12). The "linear scatter coefficient", however, which we define here as the linear attenuation coefficient excluding photoelectric absorption, is 10.7% greater than in water. There is more fluence in the .3-1.0 cm range in PMMA from unscattered I-125 radiation, and there is also more fluence from scattered photons.

An adaptation of Berger's formalism and data (3) for fluence from a point source in water was used to calculate an acrylic-to-water fluence correction factor. The method, described in Appendix A, explicitly takes into account differences in scatter due to differences in atomic composition of acrylic and water.

Fig. 5. Dose rate determined from Eq. 1 for a number of measurements at three distances from a single seed. Measurements correspond to circle radii of 3, 5, and 10 mm for the phantom block shown in Figure 2. Dose rate is measured relative to LiF TLD sensitivity to dose (water) at x-ray energy of 4 MV. Straight lines show results of least squares exponential fits to the data. Fitted value for half-life of I-125 is 59.7, 59.6 and 59.0 days for the data at 3, 5, and 10 mm, respectively.

1. Uncorrected for differences - acrylic versus water. Dose rate measured over a period of 46 days from a single seed is shown in Figure 5. A least squares fit (23) to the dose rate and I-125 decay time constant based on the 1 cm data gives a value of 7.036 cGy/hr and a half-life of 59.0 days for the seed. The manufacturer's stated calibration was 7.172 uGy-m²/hr air kerma strength (The manufacturer actually expressed seed calibration in "effective millicuries", where the air kerma strength of 1.270 cGy-cm²/h was taken to correspond to 1 effective millicurie. The number 1.270 is the product of an assumed I-125 exposure rate constant of 1.45 R-cm²/mCi-h and a W/e value for air (1,4) of 0.876 cGy/R), or 208.9 MBq (5.646 mCi) effective activity on the reference date. The published value of 59.6 days for I-125 half-life (14) gives a revised dose rate estimate of 7.005 cGy/hr, or 0.4% less. The 59.6 day half-life is used for all further calculations. The dose rate referred to here includes all corrections previously described except for the acrylic to water fluence rate correction factor. Values for A(y), for y = .3 and .5 cm, given in Table 2, also do not include the excess scatter correction for acrylic. Fitted values for the half-life of I-125 are also given in Table 2.

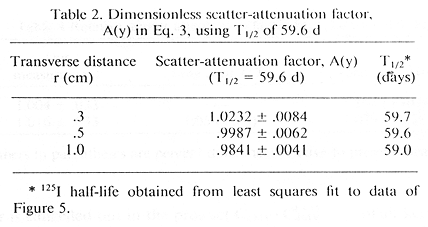
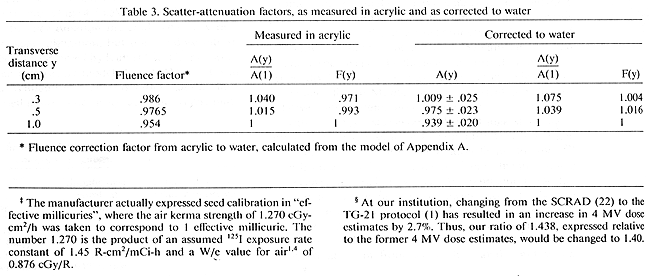
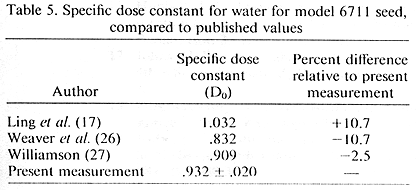
2. Corrected for relative energy fluence rate - acrylic to water. The fluence rate correction factor, calculated as described in Appendix A, is given for each measurement distance in Table 3. Relative attenuation factors, A(y)/ A(1.0) and F(y), are also given in Table 3, both with and without the excess scatter correction for acrylic. Fluence rate corrected results for F(y) are compared with values previously published for this seed in Table 4. The uncorrected specific dose constant D_o is 0.977, obtained from Eq. 4 and Tables 1 and 2. Using the excess fluence correction factor from Table 3, the specific dose constant for water is 0.932. The present measurement is compared with other published values in Table 5.

Four calibrated seeds obtained from the manufacturer over a period of 11 months were measured. Two seeds were measured extensively at I cm distance within one half-life of the seed calibration. The scatter-attenuation factors obtained from the two seeds at 1 cm agreed with each other within 0.1%, with standard errors of 0.4% and 0.7% respectively. The other two seeds were measured at all three distances, but with more than 80% of the measurements being taken between 60 and 150 days from the time of seed calibration. The mean value of A(y) determined from these seeds differed only slightly from the values in Table 2, and were in agreement within experimental error. Compared to the values in Table 2, the results differed by -0.4%, +0.1% and -0.7% at .3, .5 and 1.0 cm, respectively.

TLD sensitivity to 4 MV dose relative to dose from 70 kVp X rays was measured five times. Average standard error of the mean 70 kVp TLD reading was 1.5%, Average standard error ofthe mean 4 MV reading was 0.8%. The mean ratio of TLD response per Gy (water) at 70 kVp to TLD response per Gy (water) at 4 MV was 1.438 ±.011. Only the standard statistical error is shown, The result is 1.438 ±.018, including an estimate of ±1% for the uncertainty in ion chamber calibration. The result is similar to the value 1.42 ±0.03 obtained by Puite (21) for an 80 kVp 3.1 mm Al HVL x-ray beam, as well as the value 1.39 ±0.03 obtained by Weaver (24) for LiF powder, presumably using the Scientific Committee on Radiation Dosimetry (SCRAD) protocol (22) (At our institution, changing from the SCRAD (22) to the TG-21 protocol (1) has resulted in an increase in 4 MV dose estimates by 2.7%. Thus, our ratio of 1.438, expressed relative to the former 4 MV dose estimates, would be changed to 1.40) for megavoltage x-ray dose calibration. Absolute error in the value of this ratio due to uncertainty in 4 MV absolute calibration does not, however, affect the determination of I-125 dose rate, to the extent that the 4 MV dose is reproducible. This type of error is cancelled out in the product C_4MV * ^I-125C_4MVthat appears in Eq. 1. The I-125 dose rate is affected by the uncertainty in absolute dose calibration of the 70 kVp beam.

Positioning uncertainty and statistical variations in the TLD readings result in estimated uncertainties of ±0.8%, and ±0.4%, respectively, in dose rate at 1 cm. In Eq. 1, the quantity C_4MV * ^I-125C_4MV is uncertain to ±1.3%, and b, the ratio of TLD to acrylic attenuation is estimated to be uncertain by about ±1%. Uncertainty in the half-life contributes a dose rate error of ±.3%. Overall uncertainty, obtained by summation of errors in quadrature, is ±2.1% at 1 cm, ±2.4% at .5 cm, and ±2.5% at the .3 cm measurement point. Uncertainty in the relative scatter-attenuation factors, A(y)/A(1) and F(y), is ±3.3'% for both .5 and .3 cm measurement points.

Values for the specific dose constant for the model 6711 (silver wire) seed that have appeared in the literature are given in Table 5. The value recommended by Ling et al. (17), which is most widely used to date, is 10.7% greater than the present measurement. The value in reference (17) was based primarily on calculations, and did not take into account the effect of the 4.5 keV Ti K shell fluorescent X rays from the encapsulation material. The Ti X rays affect the exposure calibration, but not the dose rate in water, an effect first observed by Kubo (15). The phenomenon has been extensively modeled in the Monte Carlo calculation of Williamson (27), who found that the effect of the Ti K shell fluorescence is to cause an overestimate of air kerma rate and thus a reduction of the specific dose rate by 5% to 8%. The present result is 2.5% larger than the value recommended by Williamson (27).

Data recently presented by Weaver et al. (26) show a value 10.7% less than the present measurement for the specific dose constant. This would seem to be due in part to the use of a "solid water" (8) phantom by these authors. Solid water, although close to water in attenuation and depth dose characteristics (20) for I-125, has a larger photoelectric and a smaller scatter component than water in the 25-35 keV region. Applying the fluence rate correction method of Appendix A to solid water at 1 cm, one obtains the result that energy fluence rate in solid water should be multiplied by the factor 1.035 to obtain energy fluence rate in water. This factor reduces the difference, but the result in Weaver el al. (26) remains 7.6% less than the present measurement.

As seen in Table 4, previously published values of relative attenuation factor at .3 and .5 cm differ from the present determination by -20.1% to +10.0%. The estimated uncertainty in the measured ratio is ±3.3%. The present value at .5 cm agrees reasonably well with the measurement in water by Ling el al. (17), being 3.2% less than the result obtained in reference (17). Present measurernents also agree within experimental error with the Monte Carlo calculation of Williamson (27), being 0.8% greater at .3 cm and 1.9% less at .5 cm. Without the excess scatter correction, the measured ratios would be 2.4% and 4.2% lower than those obtained by Williamson at .3 and .5 cm, respectively. The fluence rate correction model of Appendix A, therefore, brings the measurement into closer agreement to the Monte Carlo (27) calculation for the relative scatter-attenuation factor in the .3-.5 cm region.

Values of A(y)/A(1) given in Table 4 suggest a smooth monotonic progression for this quantity between .3 and 1.0 cm. A(y) is a scatter-attenuation factor for the I-125 seed from which the geometrical effect of the line source has been extracted. In this sense, A(y) represents the scatter attenuation of the medium somewhat more closely than the conventional F(y), defined in Eq. 4. The value of A(1) is 0.939 ±.020, which corresponds to a dose rate 7.5% less than would be conventionally calculated for dose rate in water at 1 cm from an unattenuated point source of I-125.

Dose rate measurements from model 6711 I-125 seeds calibrated for air kerma strength have been described. The measurements, characterized by an average statistical precision of ±.6% were performed in a polymethyl methacrylate ("acrylic" or PMMA) phantom using LiF TLD detectors. TLD sensitivity was calibrated in a low energy x-ray beam, and was found to be consistent with other published values. Correction factors were applied for finite detector size and for attenuation in the TLD. A model based on Berger's data (3) for energy deposition in water from an isotropic point source was described. The model, which explicitly included differences in scatter between water and acrylic was applied to the measurements to obtain dose rate in water. The resulting dimensionless specific dose constant in water, D_o in Eq. 4 is 0.932. This value is 9.7% less than the most widely used value heretofore (17), and is close to the value recently recommended by Williamson (27) on the basis of Monte Carlo calculations. Relative dose rate measurements at .3 and .5 cm also differed from previously published calculations and measurements (6,16) by -7.8% to +25.1%, but agreed with Williamson's Monte Carlo calculation (27) within experimental error, and data of Ling et al. (17) within 3.3%.

On the basis of present data for the specific dose rate constant, we suggest that most brachytherapy treatments to date involving model 6711 I-125 seeds have overestimated treatment dose by about 10%. The use of the present value in the future is subject to possible revisions of I-125 air kerma rate calibration procedures by the National Bureau of Standards that might be introduced, for example, to exclude the effect of the low-energy X rays from the encapsulation material.

1. American Association of Physicists in Medicine (AAPM) Report no. 21, Specification of brachytherapy source strength. New York, NY: American Inst. of Physics: 1987.
2. American Association of Physicists in Medicine (AAPM). Task Group 21, Radiation Therapy Committee: a protocol for the determination of absorbed dose from high-energy photon and electron beams. Med. Phys. 10:74 1-77 1; 1983.
3. Berger, M. J. Energy deposition in water by photons from point isotropic sources. Society of Nuclear Medicine, Medical Internal Radiation Dose Committee (MIRD) pamphlet no. 2. J. Nucl. Med. (Suppl. 1): 17-25: 1969.
4. Boutillon, M.; Perroche-Roux, A.M. Re-evaluation of the W value for electrons in dry air. Phys. Med. Biol. 32:213-219; 1987.
5. Burns, G. S., Raeside, D. E. Monte Carlo simulation of the dose distribution around I-125 seeds. Med. Phys. 14:420-424: 1987.
6. Burns, G. S.; Raeside, D. E. Two-dimensional dose distribution around a commercial I-125 seed. Med. Phys. 15:56-60; 1988.
7. Chiu-Tsao, S-T.; O'Brien, K.; Sanna, R.; Tsao, H.S.; Vialotti, C.; Chang, Y-S.; Rotman, M.; Packer, S. Monte Carlo dosimetry for I-125 and Co-60 in eye plaque therapy. Med. Phys. 13:678-682; 1986.
8. Constantinou, C.; Attix, F. H.; Paliwal, B. R. A solid water phantom material for radiotherapy X ray and gamma-ray beam calibrations. Med. Phys. 9:436-441; 1982.
9. Dale, R. G. Some theoretical derivations relating to the tissue dosimetry of brachytherapy nuclides, with particular reference to iodine-125. Med. Phys. 10: 176-183; 1983.
10. Hartmann, G. H.: Schlegel, W.; Scharfenberg. H. The three dimensional dose distribution of I-125 Seeds in tissue. Phys. Med. Biol. 28:693-699. 1983.
11. Hubbell, J.H. Photon Mass Attenuation and Energy-absorption coefficlents from 1 keV to 20 MeV. Int. J. Appl. Radiat. Isot. 33:1269-1290 1982.
12. Johns, H. E.; Cunningham, J. C. The physics of radiology. 4th edition. Springfield, IL: Thornas Co; 1983: Appendix A.
13. Krishnaswamy, V. Dose distribution around an I-125 Seed source in tissue. Radiology 126:489-491; 1978.
14. Kubo, H. Determination of the half-life of I-125 encapsulated clinical seeds using a Si(Li) detector. Med. Phys. 10:889-891:1983.
15. Kubo, H. Exposure contribution from Ti K x rays produced in the titanium capsule of the clinical I-125 seed. Med, Phys. 12:215-220; 1985.
16. Ling, C. C.; Schell, M. C.; Yorke, E. D.; Palos, B. B.; Kubiatowicz, D.O. Two-dimensional dose distribution I-125 seeds. Med. Phys. 12:652-655; 1985.
17. Ling, C. C.; Yorke E. D.; Spiro, I.J.; Kubiatowicz, D.; Bennett, D. Physical dosimetry of I-125 seeds of a new design for interstitial implant. Int. J. Radiat. Oncol. Biol. Phys. 9: 1747-1752; 1983.
18. Luxton. G.; Astrahan, M. A.; Liggett, P. E.; Neblett, D. L.; Cohen, D.M.; Petrovich, Z. Dosimetric calculations and and measurements of gold plaque ophthalmic irradiators using iridium-192 and iodine-125 seeds. Int. J. Radiat. Oncol. Biol. Phys. 15:167-176: 1988.
19. Luxton, G.; Astrahan, M. A.; Petrovich, Z. Backscatter measurements from a single seed of I-125 for ophthalmic pIaque dosimetry. Med. Phys. 15:397-400; 1988.
20. Meigooni, A. S.; Meli, J. A.; Nath, R. A comparison of solid phantoms with water for dosimetry of I-125 brachytherapy sources. Med. Phys. 15:695-701; 1988.
21. Puite, K. J.; A thermoluminescence system for the intercomparison of absorbed dose and radiation quality of X rays with a HVL of O.1 to 3.0 mm Cu. Phys. Med. Biol. 21: 216-225; 1976.
22. Scientific committee on radiation dosimetry (SCRAD) of the American Association of Physicists in Medicine. Protocol for the dosimetry of x- and gamma-ray beams with maximum energies between 0.6 and 50 MeV. Phys. Med. Biol. 16:379-396; 1971.
23. Turbo Numerical Methods Toolbox. Scotts Valley CA: Borland International: 1986.
24. Weaver, K. A. Response of LiF powder to I-125 photons. Med. Phys. 11:850-854; 1984.
25. Weaver, K. A. The dosimetry of I-125 seed eye plaques. Med. Phys. 13:78-83; 1986.
26. Weaver, K.; Barnett, C.; Huang, D.; Ling, C.; Schell, M; Smith, V. Dosimetric parameters for I-125 and Ir-192 sources (Abstr.). Phys. Med. Biol. 33(Supp1. 1): 153; 1988.
27. Williamson, J. F. Monte Carlo evaluation of specific dose constants in water for I-125 seeds. Med. Phys. 15:686-694; 1988.

The fluence rate in water from a point source is represented (3) as a product of a polynomial and exponential in the dimensionless variable μx where x is the distance and μ is the linear attenuation coefficient.

The polynomial coefficients, which represent the "buildup factor" are given by Berger (3) for an isotropic point source in water for different x-ray energies. The polynomial coefficients in reference (3) are identified as being proportional to the scatter function.

The fluence in acrylic is represented here by the same expression, with the replacement of the linear attenuation coefficient for water with that for acrylic, and scaling the polynomial coefficients a_n by the following substitution:

The I-125 energy spectrum from Ling el al. (17), including silver fluorescence X rays was used to calculate relative energy fluence rate in water compared to acrylic. Results for the fluence ratio calculated for the measurement distances from Eqs. A.I and A.2 are given in the second column of Table 3.

Acknowledgements-The authors would like to express their appreciation to Michael Sapozink, M.D., Ph.D. for his comments conuerning the manuscript and to an anonymous reviewer whose questions and suggestions contributed greatly towards improving the clarity of the presentation.