Dosimetric Calculations and Measurements of Gold Plaque Ophthalmic Irradiators using Iridium-192 and Iodine-125 Seeds
Gary Luxton, PH.D.,1 Melvin A. Astrahan, PH.D.,1 Peter E. Liggett, M.D.,2 David L. Neblett, M.S.E.E.,1 Dierdre M. Cohen, M.D1 and Zbigniew Petrovich, M.D.1
Int. J Radiation Oncology Biol. Phys., Vol. 15, pp. 167-176, Copyright 1988 Pergamon Press
(1)Department of Radiation Oncology
(2)Department of Ophthalmology
University of Southern California Medical School, Los Angeles, CA 90033
ABSTRACT
The dosimetry of ophthalmic plaques designed to hold iridium-192 or iodine-125 seeds is investigated experimentally and by means of a computer model. A phantom for thermoluminescent dosimetry (TLD) which permits measurements to within 2 mm of the plaque surface is described. TLD data are compared with model calculations that take into account the active length of the seeds, anisotropy of dose distribution from single seeds, and scatter within the phantom. An isotropic point source calculational model is accurate for clinical calculations, particularly at depths greater than 5 mm. Relative central axis dose measurements for I-125 in a gold plaque are also in agreement with the model. Comparisons of Ir-192, I-125 and Co-60 plaques are presented. The relative advantages of using these isotopes in eye plaques are discussed.
Brachytherapy, Dosimetry, Ophthalmic irradiation, Choroidal melanoma, Iridium-192.
Accepted for publication 1 February 1988
INTRODUCTION
Removable episcleral plaques containing radioactive material have been used for many years in the management of ophthalmic tumors such as choroidal melanoma and retinoblastoma. This treatment provides an attractive alternative to enucleation. Ophthalmic plaque radiotherapy allows higher doses to be delivered to the tumor with greater sparing of noninvolved tissues compared to X ray teletherapy. The technique is less expensive and generally more accessible than heavy charged particle teletherapy (3,7). Late complications from treatment with episcleral radioactive plaques, however, are common (4,17,20). Complications take the form of retinopathy, scleral necrosis, cataracts, and glaucoma. Also, there is relatively little success treating tumors that present with a height larger than 8 mm (17). Obtaining precise dosimetry for ophthalmic plaques within a few millimeters of the plaque surface is of interest because, such data may correlate strongly with complications of treatment.
Historically, Co-60 plaques (20,21) have been most commonly used. Cobalt-60 plaques, however, pose certain difficulties because of the high energy of the associated gamma radiation. The plaques are difficult to shield, and present a hazard to both patient and attending staff. Calculations and measurements have been published (1,2,13) for the Co-60 plaques (The Radiochemical Centre Ltd, Amersham, U.K.) developed by Stallard (21). The dose distribution from Co-60 plaques is not optimal since the penetrating radiation from this isotope may deliver considerable dose to uninvolved structures such as the lens, retina, optic nerve, and contralateral eye. In ophthalmic plaque radiotherapy, other isotopes that have been used in place of Co-60 include iodine-125 (16), ruthenium-106 (12), gold-198 (17), tantalum-182 (17), and iridium-192 (17). A purpose of the present work is to measure absorbed doses of Ir-192 and I-125 ophthalmic plaques, and thereby test a simplified dose computational algorithm. This algorithm is then used to compare dose distributions about plaques using Ir-192, I-125, and Co-60.
The Ir-192 and I-125 plaques presented here differ dosimetrically from Co-60 foil plaques. The discrete seed form of the radioactive material for Ir-192 and I-125 is dosimetrically important because there is considerable dose rate reduction along the longitudinal as compared to the transverse direction ()11,23). Also, the low energy of I-125 radiations leads to more rapid dose decrease with distance from the source for this isotope as compared to Co-60. Another difference that has been observed is that gold foil backing of I-125 caused an apparent dose rate reduction of approximately 8% (22).
METHODS AND MATERIALS
Plaque design and construction
Plaques are cast in a gold alloy as sections of a spherical shell, 25 mm in diameter, 1.5 mm thick, by the lost wax technique. Some examples are shown in Figure 1. Each casting includes a pattern of grooves embedded in the concave surface of the gold shell which are used as receptacles for radioactive seeds of Ir-192 or I-125. For most plaques, the source holders are arranged in a radial rather than a circular or rectangular array, because more sources can be distributed over the plaque surface. This reduces the individual seed strength required for a given total activity, since excessively high seed activity could potentially lead to treatment complications. Gold was chosen for biological inertness and shielding advantages.
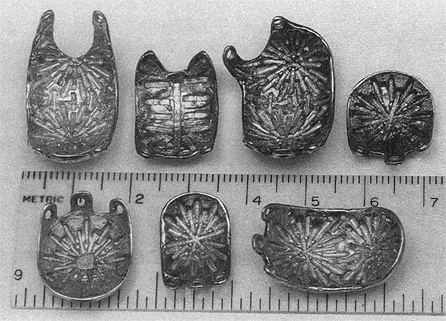
|
Fig. 1. Several episcleral plaques used at the University of Southern California. The plaques are cast from gold as a 1.5 mm thick portion of a spherical shell. Each plaque has a pattern of grooves to hold either Ir-192 or I-125 seeds and eyelets for suturing the plaque to the sclera.
|
The lost wax or investment casting technique is a method widely used by jewelers for precision casting using expendable wax patterns. First, a wax model of the desired gold eye plaque is made. Next, a mold is made of this wax model by embedding it in a fine plaster cell investment. The plaster investment is then heated and the wax burned out ("lost wax"), leaving a cavity with the shape of the desired eye plaque. Gold is then poured into the cavity through separate holes that were created by attaching wax wire (sprue) to the wax eye plaque model. A vacuum is used to remove air from the cavity, causing the mold to be completely filled with the casting metal. The investment is then broken apart to release the gold eye plaque. Additional wax models are fabricated by injecting wax into a rubber mold made from the gold plaque. Wax models can be modified to enable optimization of treatment delivery. Custom plaques, such as those notched to enable placement next to the optic nerve, are produced by modifying a wax model which is then cast in gold.
TLD Measurements ofplaque dose distributions
Phantom and dosimeter description. Measurements were made using 1 mm diameter cylindrical LiF thermoluminescent dosimeter (TLD) rods, 3 mm in length (TLD-100, Harshaw/Filtrol, Solon, OH). Rods were placed in holes in a hemispherical eye phantom, 25 mm in diameter, cast in an epoxy resin (Fibre Glass-Evercoat Co., Inc., Cincinnati, OH, Diglycidyl ether of bisphenol A (50%), mixed aliphate amines (50%)), the density of which was measured to be 1.12 g/cm³ . The phantom (Fig. 2) was drilled with holes aligned in a plane bisecting its base. Hole diameter was approximately 1 mm, just large enough to accommodate the TLD rods. The distance of each TLD from the plaque along the central axis was determined radiographically. Using metal stylets to image the TLD locations, we determined central axis depths for the dosimeters to an accuracy estimated to be within ±0.1 mm.
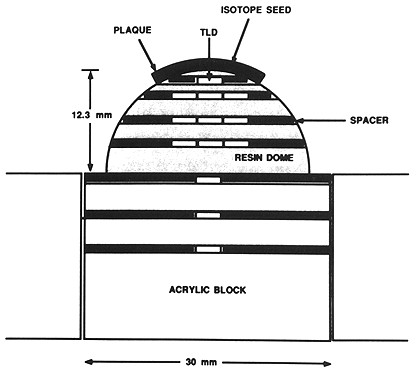
|
Fig. 2. Diagram of the phantom used for TLD measurements. The hemispherical dome is cast from an epoxy resin. The rectangular pieces are acrylic. Nylon spacers are used to align TLD's.
|
The eye phantom was placed on a machined rectangular acrylic block as shown in Figure 2. Holes for TLD rods were drilled through the underlying block as well, in the same vertical plane as those in the hemispherical eye phantom. The plaque suture eyelets were placed on locating pins to assure reproducibility of plaque positioning. Nylon spacers placed at both ends of the holes served to center the TLD rods on the central axis of the plaque.
TLD measurement technique. TLD rods were initially sorted into groups of equal sensitivity to within ±3% by measuring the light output from each rod after exposure to a dose of 1 Gy using a 4 MV X ray beam. Rods were annealed within their respective groups according to standard procedures: 400°C for 1 hr prior to exposure and 15 min. at I05°C prior to readout. For each radiation exposure, only TLD's from within a single group were used, and a dose calibration was obtained by exposing at least 5 TLDs from the group to I Gy of 4 MV radiation. The variation in readings among the calibration TLD's was consistent with maintenance of uniform sensitivity within the group. The TLD sorting procedure was, however, repeated on several occasions when it appeared that there might be significant variation within a group. Sensitivity to 4 MV dose was used as a relative calibration factor for I-125 measurements and directly as a calibration factor for Ir-192 dose measurements. Energy independence for TLD-100 between Ir-192 and 4 MV is suggested by calculations of photon energy dependence reviewed by Horowitz (8). An average difference of less than 1% in the mass energy absorption coefficient of LiF relative to air for photons of energy between 150 and 600 keV compared to Co-60 is noted by Horowitz (8, Table 1).
Several unexposed rods were read out for each run to allow subtraction of background. The background, which depended upon the particular measurement, varied from less than 0.1% to no more than a few percent. Exposure times in the phantom were typically 1-3 hours. Measurements were repeated up to 23 times to improve statistical precision. Mean values, experimental standard deviations and 95% confidence limits (obtained from the t distribution) were calculated from the data.
Ir-192 seed calibration. To test for accuracy the dose computation algorithm for eye plaque dosimetry, dose rate was measured from calibrated seeds. Since individually calibrated seeds were not readily available, several lr-192 seeds were calibrated by a method that is now described. Dose rate was measured from a group of seeds using an NBS-traceable thimble type ionization chamber (0.6 cm³). The chamber was placed in the center of a polystyrene phantom drilled to fit the thimble. The ionization chamber had been calibrated at Co-60 energy as well as in a 250 kVp, 3.0 mm Cu HVL X ray beam. The reported exposure calibration factor at 250 kVp was lower by 1.7% than the Co-60 calibration factor used for the Ir-192 measurements. A group of seeds was distributed in a concentric circular groove of radius 2.55 cm. Using a group rather than a single seed improved the signal-to-noise ratio so that the precision of the measurement was 1-2%. The measurement was converted to dose rate at 1 cm using the inverse square distance factor modified by a polynomial. The polynomial in the distance variable was taken from the Monte Carlo calculations of Dale (6) of dose rate in water. The polynomial of Meisberger et al. (14) would give a dose rate at 1 cm that is 1.7% larger. Individual seed activities, expressed in the form of dose rate at 1 cm in water, were obtained by comparing all of the individual seeds using a well type ionization chamber (Model CRC-5R, Capintec Corp., Ramsey, NJ). A displacement factor of 1.00 was used for the thimble, based on the rationale that the polynomials of both Dale (6) and Meisberger et al. (14) change by less than 0.3% as the distance decreases by 3 mm, the inner radius of the thimble. No adjustment to the calibration factors was made for the use of polystyrene rather than water since the linear attenuation coefficient in polystyrene is within I% of that in water for Ir-192 photons.
Computer dose calculation model
The basic algorithm of the dose calculation model treats each Ir-192 and I-125 seed as an unfiltered line source 3 mm in length, located at the geometrical center of the physical source, modified by attenuation scatter and oblique filtration factors. Ir-192 seeds (Alpha Omega Services, Inc., Paramount, CA) are 0.5 mm diameter, 3 mm length with an active volume 0.3 mm diameter and slightly less than 3 mm in length. I-125 seeds (Model 6711, 3M Corp., Medical Products Division, St. Paul, MN) are 0.8 mm diameter, 4.5 mm length with an active volume 0.5 mm diameter and 3 mm in length. The unfiltered line source approximation enables dose rate from each seed to be expressed as a standard geometrical factor, as in Eq. (1) below.
D(r,x) = S * A(r) - F(θ) * (1/L) * (1/r) * [arctan((x + L/2)/r) - arctan((x - L/2)/r)] (1)
where
D(r,x)
S
r
L
x
A(r)
F(θ)
|
is the dose rate (Gy/hr)
is seed strength, expressed as dose rate I cm transverse to the seed in water (Gy cm²/hr)
is transverse distance from the seed center (cm)
is active length of the seed (cm)
is longitudinal distance from the center of the seed (cm)
is the attenuation scatter factor for transverse distance
is the anisotropy factor as a function of angle θ = arctan (|x|/r).
|
To account for attenuation and scatter in the phantom and anisotropy effects due to oblique filtration, the unfiltered line source function is multiplied by distance and angular factors respectively. For Ir-192, the effective angular factor F(θ) is taken from the Sievert integral calculation by Williamson et al. (23) for dose rate at 10 cm in air as a function of angle for seeds of this design. The radial dose rate factor A(r) is taken from the polynomial fit to the Monte Carlo calculation of Dale (6) for a point source in water as described above under seed calibration. The radial factor differs from 1.00 by less than 2% for Ir-192 within 20 mm of the source. For I-125, lookup tables based on measurements of Ling et al. (11) for the same model I-125 seeds in water were used for both radial and angular factors.
For comparison of dose calculations with TLD measurements, the TLD data are transformed into point measurements referred to the center of the TLD rods. This is done by calculating dose rate at the center of the detector as well as averaged over a 3 mm line detector. The measurements are then multiplied by the ratio of the two calculations. No correction is made for the use of acrylic rather than water. The linear attenuation coefficient for acrylic is approximately 14% larger (9) than for water at Ir-192 energy. The probability of interaction per cm of water is approximately 11% (9), and so the dosimetric correction in the 10-20 mm range would be expected to be about 2%.
For comparative dosimetry of gamma ray isotopes in the same geometry and using the same method of calculation, a model using hypothetical 3 mm length, line source Co-60 "seeds" is used. For these calculations, as for Ir-192, the radial dose factor is taken from the point source Monte Carlo of Dale (6), with the angular factor taken to be unity. The use of a constant for the angular factor may be justified by noting that 5 mm from the center of a Co-60 "seed", the Sievert integral (19) calculation is only 3% less at an inclination of 70° compared to an unfiltered line source.
RESULTS AND DISCUSSION
Calibrated single seed of Ir-192 in acrylic phantom
To test the validity of the measurement system for Ir-192, a single calibrated seed was placed in a hole drilled in an acrylic block as in the lower part of Figure 2. The block was surrounded by acrylic on all sides. Measurements of dose rate are shown in Figure 3 for five distances perpendicular to the seed axis, between 1.9 and 10.2 mm. Measurements are taken at five displacements along the seed axis between 0 and 12 mm. Error bars designate 95% confidence limits of the data. The curves represent the calculations of the model.
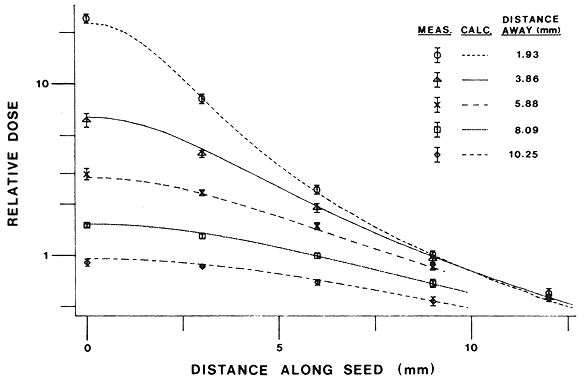
Fig. 3. Measured dose distribution of a single calibrated seed of "'IT in the rectangular acrylic phantom compared to calculated values. Seed activity has been scaled for a calculated dose of unity at a distance of 10 mm transverse to the seed. Measurements along lines parallel to the seed axis for several transverse distances are shown as data points with 95% confidence limits. Calculated dose profiles are designated by solid and broken lines.
All but one of the 22 measurements overlap the model calculation within the 95% confidence limits of measurement. One such disagreement would be expected on the average, on the basis of statistics alone. The largest fractional difference occurs at the point 12.0 mm "along", 1.9 mm "away" from the seed, where the measurement exceeds the model calculation by 9.5%. Use of published Monte Carlo (23) rather than Sievert integral (13) estimates for the angular factor would increase dose underestimation by the model to 22% at this point and to 17% instead of 1.9% for the adjacent measurement. Averaged over all 22 measurements, the ratio of measured to calculated value is 0.993 ± .041. The close agreement between measurement and calculation for this case and for the case with four calibrated seeds in a gold plaque described below strongly supports the usefulness of both the measurement system and the calculational model for Ir-192.
Gold plaque with four calibrated seeds of Ir-192
Four calibrated Ir-192 seeds of equal activity (within ±0.5%) were placed radially in a gold plaque. Calculated and measured central axis dose rates are shown in Figure 4. Also shown are the 95% confidence limits for the measured data. The mean ratio of measurement to calculation is 0.983 ± 0.030. Estimated uncertainty in the Ir-192 seed calibration is ± 3%.
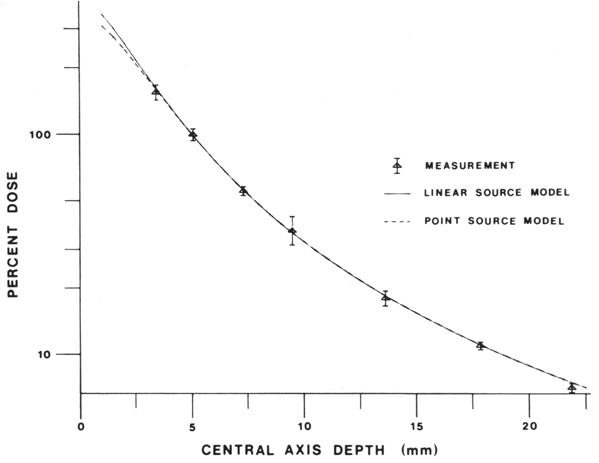
Fig. 4. Measured central axis dose for a plaque with 4 calibrated seeds of Ir-192 compared with calculated values. Measurements are shown as data points with 95% confidence limits. Calculations are shown for both point source and linear source computer models.
The only measurement point that appears to significantly differ from the calculation is at 22 mm depth along the central axis. For this point the measurement is 5.4% less than the calculation, with a standard error of 2.2%. In the interest of simplicity, all calculations were done for water. Taking into account the phantom material in a simple linear attenuation model, however, would reduce the calculated value for the 22 mm point by approximately 2.5%, and thereby reduce the discrepancy to insignificance. Since the same model without modification is in agreement with absolute measurements both with and without a gold plaque (Figs. 3 and 4), it appears that the gold plaque does not appreciably change the dosimetry from that of a full scatter geometry for Ir-192.
Clinical procedure: Plaque with 18 seeds of Ir-192
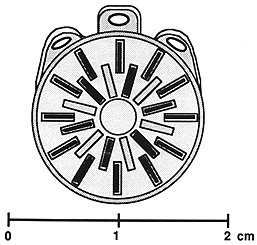
A set of measurements and calculations was carried out for a clinical procedure with a plaque containing 18 seeds of Ir-192. The plaque is shown in Figure 5. Seed strength of 0.0254 Gy cm²/hr was estimated from data supplied by the manufacturer. Seeds were assumed to all have the same activity. The results are shown in Figure 6. The calculated dose rate at 5 mm depth along the central axis was 1. 1 Gy/hr, taken as 100%. Calculated and measured dose profiles are shown at four depths along the central axis between 3.4 and 9.5 mm. Standard deviations are shown with the mean values, which were obtained from three samples at each point.
|
Fig. 5. Diagram of the plaque and seed distribution used in a typical clinical procedure. The plaque contains 18 seeds of Ir-192. The distribution is symmetrical: six seeds positioned radially at 60° increments centered on a 3 mm radius circle, and 12 seeds positioned radially at 30° increments centered on a 5.5 mm radius circle.
|
Central axis dose calculations and measurements are shown in Figure 7. Also shown for comparison is the dose distribution from a multiple point source model with no adjustment for anisotropy. Further calculations show that the maximum internal scleral dose rate, defined as the dose rate I mm from the plaque surface in contact with the external sclera, is 3.6 Gy/hr and occurs 4 mm off axis. This is 33% larger than the central axis value. The maximum is displaced because, as illustrated in Figure 5, the seeds are all displaced from the axis.
There is adequate agreement for clinical purposes between the measurements and the model. The measurements display some asymmetry, particularly at the two smaller depths. This may be due in part to variations in activity among the 18 seeds. Activity variations are commonly present in a batch of Ir-192 seeds taken from the same manufacturer's lot number. For example, in one group of 36 seeds from this manufacturer assayed in the well chamber, the standard deviation was found to be 7.2%, with activities ranging from -13% to +18% relative to the mean. Individual assay of each seed with seed selection for uniformity of activity, could remove this source of uncertainty.
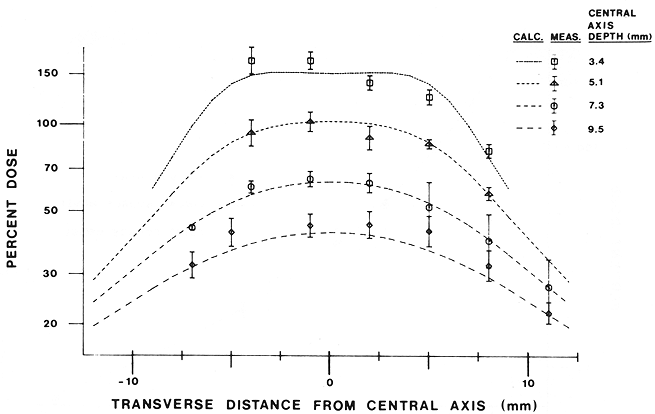
Fig 6. Profile calculations and measurements at various distances from the Ir-192 plaoue illustrated in Figure 5.
Isotropic point source model for central axis dose calculations
The standard isotropic point source model calculation of central axis dose rate was compared with the line source model for two examples of Ir-192 plaques (Figs. 4 and 7). It is apparent that the two models give identical results for all practical purposes, at depths greater than 5 mm on the central axis. In both examples, however, the point source model gives a dose rate approximately 8% less than the line source model at 1 mm depth. The relative magnitude of the dose rates calculated by the two models in the proximal region depends, however, on the particular seed locations used. For example, for a seed on the central axis, dose rate in the point source model is greater by 35% at the 1 mm depth.
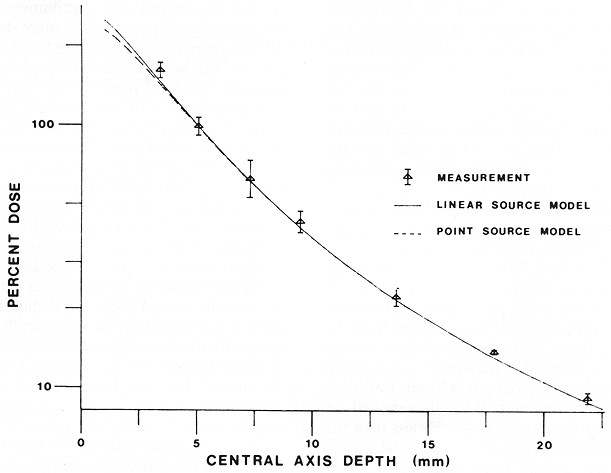
Fig. 7. Measured central axis dose for the plaque described in Figure 5 compared with calculated values. Measurements are displayed as data points together with experimental standard deviation. Seed activity has been scaled for a calculated dose of 100% at a point on the central axis 5 mm from the plaque. Calculations are shown for both point source and linear source computer models.
I-125 measurements
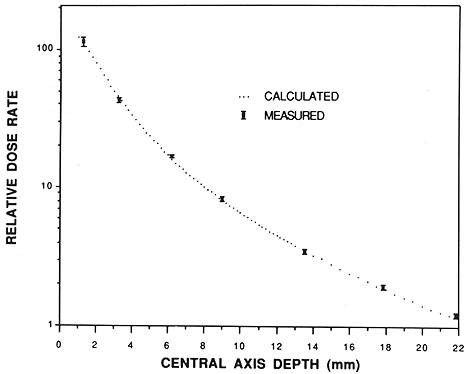
To test the applicability of relative dose rate calculations for I-125 seeds in a gold plaque, measurements were made on a plaque containing two model 6711 I-125 seeds of equal activity. The seeds were glued into the plaque with their centers positioned approximately 2 mm on either side of the central axis. A series of dose rate measurements, based on TLD sensitivity to 4 MV dose, was made for seven depths on the central axis in the cast resin + acrylic phantom. The dose rates were referred to a fixed date using a half life of 59.6 days (10). Measurements were repeated 20 times. The central axis dose rate calculations and measurements are shown in Figure 8. The dots in Figure 8 represent calculations at discrete depths, whereas the plotting symbols represent the measurements. Relative normalization was adjusted to obtain the best fit between calculations and measurements.
|
Fig. 8. Calculations compared to measurements of relative central axis dose rate in the phantom of Figure 2 from a gold plaque containing two seeds of I-125. The dots represent discrete calculations. Plotting symbols represent the measurements with error bars designating 95% confidence limits.
|
Relative central axis dose measurements for two seeds of model 6711 I-125 in a gold plaque on the resin phantom show agreement with computer calculations based on published water phantom measurements. Dose normalization, however, was obtained empirically. Dose from I-125 depends strongly on tissue type. Monte Carlo calculations of Chui-Tsao et al. (5), for example, for a point source of I-125 show a depth-dependent variation from 125% to 90% for dose in water relative to dose in homogenized eye medium between 0 and 25 mm from the source. The present result shows no apparent variation with depth to 22 mm for dose in a tissue like medium compared to a simplified model calculation for dose in water. Dose uncertainty due to tissue type variations within the eye must, however, be considered to be present for dose from I-125 plaques.
Calculational comparison of Ir-192, I-125, and Co-60 plaques
Central axis dose rates are plotted in Figure 9 for identical plaques 15 mm physical diameter, 13.5 mm active diameter, containing seeds of I-125 and Ir-192. Also plotted are central axis data taken from the calculations of Chan et al (2) for the Stallard Co-60 CKA-4 applicator. To permit a dosimetric comparison of the isotopes using the same method of calculation, we also plot central axis dose rate for a plaque with the same geometry as for Ir-192, but containing hypothetical Co-60 unfiltered line sources instead. The plaque is the one illustrated in Fig. 5 with only the outer 12 seed slots filled. All cases are normalized to 100% at 5 mm depth on the central axis.
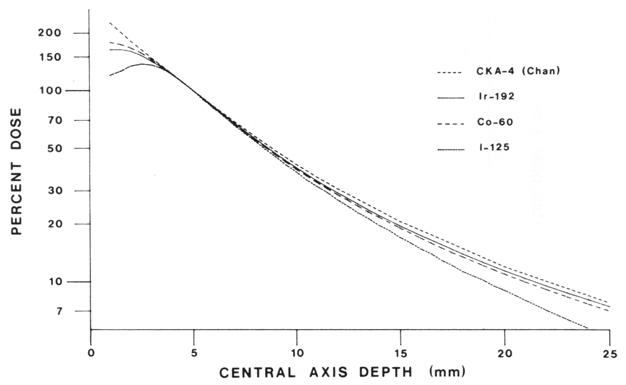
Fig. 9. Calculated central axis dose distributions for a plaque similar to that illustrated in figure 5 containing 12 Ir-192, I-125 or hypothetical Co-60 seeds in the outermost ring. Central axis calculation (Chan et al (2)) for the CKA-4 Co-60 plaque is also shown.
From the central axis dose rate distributions of Figure 9, we see that dose rate decreases somewhat more rapidly at distances greater than 8 mm from the plaque for I-125, as compared to Ir-192 and Co-60. At 25 mm from the plaque, the dose rate relative to 5 mm is 31 % less for I-125 than for Ir-192. Over the range 10-25 mm, relative dose rate from the Ir-192 plaque is 1%-5% greater than from the Co-60 line sources plaque. A smaller rate of decrease with distance for Ir-192 is observed in the model, compared to Co-60. This feature was observed both in Monte Carlo calculations (6) and in measurements (14). Over the range 10-25 mm, the Ir-192 relative dose rate is 4%-5% less than the CKA-4 Co-60 plaque data of Chan et al. (2). The higher relative dose rates seen for the CKA-4 reflect the assumptions in the calculational method in Chan et al., wherein no allowance was made for tissue attenuation. The CKA-4 calculation of Magnus (13), however, included a factor for tissue attenuation. Relative central axis dose rate for the CKA-4 from Magnus (13) ranges from a maximum of 3% greater dose rate at 10 mm to I% less at 25 mm than the present Ir-192 plaque. The central axis dose rate curve from the Ir-192 plaque over the 5-25 mm range is almost indistinguishable from the Co-60 central axis dosimetry of Magnus for the CKA-4 plaque.
In the region from I to 4 mm, differences are seen among the central axis distributions. The Co-60 line sources calculation gives 48% more dose rate than I-125 and 9% more than Ir-192 at a depth of 1 mm. Higher dose for the Co-60 "seeds" occurred with the presence of attenuation factors for Ir-192 and I-125 but not for Co-60 . The relative central axis dose rate for the CKA-4 plaque from Chan et al. (2) and Magnus (13) is 25% higher than the Co-60 line sources calculation. This is due to the presence of radioactive material in closer proximity to the central axis for the CKA-4. Off axis, directly under a Co-60 line source, relative dose rates at 1-2 mm depth are similar to those of the CKA-4 for points on the central axis.
Isodose distributions for plaques with Ir-192 and I-125 seeds are given in Figure 10, superimposed on a drawing of the eye. Shown for comparison is the isodose distribution for the CKA-4 taken from Chan et al. (2). Dose rates are normalized to 100% at 5 mm depth along the central axis. With the plaque placed near the posterior pole there is approximately 25% less dose to the lens for I-125 than for either Ir-192 or the Co-60 CKA-4 plaques. Transverse dose fall-off for both Ir-192 and I-125 are more rapid. For example, the 70% isodose line crosses the sclera 1.0 mm closer to the central axis for I-125 and 0.7 mm. closer for Ir-192. Since the active radius of the seeds plaques is approximately 0.7 mm smaller than the CKA-4, however, the decrease in the width of the isodose distribution appears to be only weakly dependent upon the type of isotope.
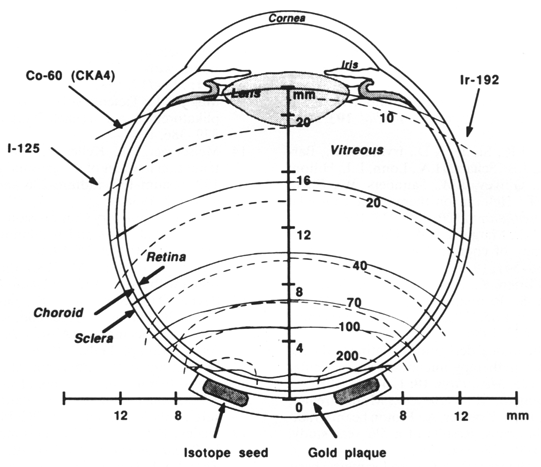
Fig. 10. Isodose distributions calculated for plaques similar to Figure 5, containing 12 seeds of Ir-192 or I-125 in the outer ring. Isodose lines for the two radioisotopes are shown as broken lines overlayed on the two sides of a diagram of the eye to illustrate the scale. Continuous lines denote the isodose distribution for the CKA-4 Co-60 plaque, taken from Chan et al. (2). Dose distributions are normalized to 100% on the central axis, 5 mm from the plaque.
CONCLUSIONS
Dosimetric investigations have shown that the use of either Ir-192 or I-125 seeds in a gold plaque are viable alternatives to Co-60 plaque therapy. There is no significant dosimetric contraindication for using either type of radionuclide in place of Co-60 for ophthalmic tumors up to 10 mm thickness. If it is desired to use plaque therapy for larger tumors, then Ir-192 may be preferred over I-125, the dose being approximately 15% greater at a depth of 15 mm relative to that at 5 mm. There are no inherent dosimetric differences between Co-60 and Ir-192 sources. Differences in the dose distributions near the sources arise from differences in encapsulation or geometric arrangements of Co-60 and Ir-192 sources. For comparable apical dose with the plaque design presented here, there is typically 25% less central axis scleral dose from I-125 seed than from Co-60 plaques. This is largely due to the self-shielding effects close to the ends of I-125 seeds. Despite the dose sparing along the central axis, the maximum scleral doses are approximately the same for all three isotopes relative to dose at 5 mm depth along the central axis.
Advantages of Ir-192 and I-125 over Co-60 plaques include greater ease of customizing the plaque for individual patients, both physically and dosimetrically. Also, there is a smaller radiation safety problem in shielding the plaque, particularly for I-125 . Exposure rate measurements of Ir-192 and I-125 seeds showed that a typical gold plaque reduced the exposure rate compared to no plaque by 40% from Ir-192 and by 97% from I-125 . The exposure rate from I-125 was not reduced further because of backscatter from the phantom.
It has not heretofore been necessary to hospitalize I-125 patients for the duration of the treatment. Lightweight lead eye shields of 0.5 mm thickness sufficed to reduce exposure rate from all patients in our experience to less than 1 mr/hr at 1 m. Patients may therefore be released with relatively few restrictions as per the recommendations of NCRP 37. 18 New rules and regulations of the United States Nuclear Regulatory Commission (7) however, have restricted this practice.
An advantage Co-60 plaques is that they are prefabricated and available commercially. Another advantage is that they have a relatively long useful life, corresponding to the 5.3 yr half-life of the isotope. The foil plaques may furthermore be presumed to have a high degree of uniformity of activity, which is not always the case among a group of seeds of I-125 and Ir-192. Co-60 shares with Ir-192 the property that tissue doses are virtually independent of tissue type, unlike I-125. Indeed, for this reason, absolute tissue doses from I-125 plaques must be considered to be somewhat uncertain at this time. Advantages in dose distribution and radiation protection from I-125 plaques, however, strongly commend their use in preference to the other radionuclides discussed for tumors to a height of 12 mm.
Finally, dose calculations for Ir-192 applicators show close agreement with central axis and profile measurements. Comparison with isotropic point source model calculations show that the simplified model gives acceptable accuracy when seed locations are precisely known. The point source model is accurate for distances greater than 5 mm from the plaque surface.
REFERENCES
- 1. Casebow, M.P.: The calculation and measurement of exposure distributions from Co-60 ophthalmic applicators. Br. J Radiol. 44: 618-624, 1971.
- Chan, B., Rotman, M., Randall, G.J.: Computerized dosimetry of Co-60 ophthamic applicators. Radiol. 103: 705707, 1972.
- Char, D.H., Castro, J.R., Stone, R.D., Irvine, A.R., Barricks, M., Crawford, J.B., Schatz, H.A., Lonn, L.I., Hilton, G.F., Schwartz, A., Quivey, J.M., Saunders, W., Chen, G.T.Y., Lyman, J.T.: Helium ion therapy for choroidal melanoma. Arch. Ophthalmol. 100: 935-938, 1982.
- Char, D.H., Lonn, L.I., Margolis, L.W.: Complications of cobalt plaque therapy of choroidal melanomas. Am. J Ophthalmol. 84:536-541, 1977.
- Chiu-Tsao, S-T., O'Brien, K., Sanna, R., Tsao, H-S., Vialotti, C., Chang, Y-S., Rotman, M., Packer, S.: Monte Carlo dosimetry for I-125 and Co-60 in eye plaque therapy. Med. Phys. 13:678-682,1986.
- Dale, R.G.: Some theoretical derivations relating to the tissue dosimetry of brachytherapy nuclides, with particular reference to iodine-125. Med. Phys. 10: 176-183, 1983.
- Gragoudas, E.S., Goitein, M., Verhey, L., Munzenreider, J.E., Urie, M., Suit, H.D., Koehler, A.: Proton beam irradiation of uveal melanomas; Results of a 51/2 year study. Arch. Ophthalmol. 100: 928-934, 1982.
- Horowitz, Y.S.: The theoretical and microdosimetric basis of thermoluminescence and applications to dosimetry. Phys. Med. Biol. 26: 765-824, 1981.
- Johns, H.E., Cunningham, J.C.: The Physics ofRadiology, 4th edition. Springfield, IL, Thomas, 1983.
- Kubo, H.: Determination of the half-life of 1- 12 5 encapsulated clinical seeds using a Si(Li) detector. Med. Phys. 10: 889-891, 1983.
- Ling, C.C., Yorke, E.D., Spiro, U., Kubiatowicz, D., Bennett, D.: Physical dosimetry of I-125 seeds of a new design 23.for interstitial implant. Int. J. Radial. Oncol. Biol. Phys. 9:1747-1752,1983.
- Lommatzsch, P.K.: Beta irradiation of choroidal melanoma with Ru-106/Rh-106 applicators. Arch. Ophthalmol. 101:713717,1983.
- Magnus, L.: Tiefendosisberechnung fur die 61 Co-Augenapplikatoren CKA 1-4 (nach Stallard). Strahlentherapie 132: 379-386,1967.
- Meisberger, L.L., Keller, R., Shalek, R.J.: The effective attenuation in water of the gamma rays of gold- 198, iridium192, cesium-137, radium-226 and cobalt-60. Radiol. 90: 953-957,1968.
- Nuclear Regulatory Commission: Medical uses of byproduct material; rules and regulations. Federal Register 51: 3695936960, Oct. 16, 1986.
- Packer, S., Rotman, M.: Radiotherapy of choroidal melanoma with iodine- 125. Ophthalmol. 87: 5 82-590, 1980.
- Payne, D.G., Simpson, E.R., Japp, B., Fitzpatrick, P.J., Gallie, B., Palvin, J.: Experience with plaque irradiation of choroidal melanomas (Abstr.). Int. J. Radial. Oncol. Biol. Phys. 12(Suppl. 1): 122, 1986.
- Precautions in the management of patients who have received therapeutic amounts of radionuclides. Report No. 37, National Council on Radiation Protection and Measurements. Washington, NCRP Publications, 1970.
- Shalek, R.J., Stovall, M.: Dosimetry in implant therapy, In Radiation Dosimetry, Vol. III, 2nd edition, Attix, F.H., Tochilin, E. (Eds.). New York, Academic Press. 1969, pp. 743-807.
- Shields, J.A., Augsburger, J.J., Brady, L.W., Day, J.L.: Cobalt plaque therapy of posterior uveal melanomas. Ophthalmol. 89: 1201-1207, 1982.
- Stallard, H.B.: Radiotherapy for malignant melanoma of the choroid. Brit. J Ophthalmol. 50: 147-155, 1966.
- Weaver, K.A.: The dosimetry of I-125 seed eye plaques. Med. Phys. 13:78-83, 1986.
- Williamson, J.F., Morin, R.L., Khan, F.M.: Monte Carlo evaluation of the Sievert integral for brachytherapy dosimetry. Phys. Med. Biol. 28: 1021-1032, 1983.
Plaque Simulator References |
Guide Contents









